UPCOMING: June 16-22 2025 ~ (Rotterdam, the Netherlands) :: LIVE in WORM :: HAROLD SCHELLINX Post-Post ULTRA (van 1983 tot en dan almaar verdur) :: (it is all) Politics >:> eternity, unPublic, sudoku's, Commuters, 1024, k7, collage, Gentle Slaughter ... Concert on Saturday, June 21. Drinks on Sunday 22!!
SUBSCRIBE to soundblog_un_public our personal / private old-school email newsletter alternative to the use of FB, X, Insta and other surveilling & exploiting media. Our occasional newsletter brings web links to new and not-so-new thoughts, to releases, concert dates, texts related to projects / works by Har$, the ookoi, other collabs, etc.
[ quicknav-: Permutation Matrices | Sudoku Dream Machine | war drift (sudoku 4, for violoncello) | costas sudokus | 3d sudokus ]
15 mins read 🤓
‘War drift’ for violoncello, and other sudoku, latin and costas grids
january 23, 2025
Permutation matrices
A permutation matrix (of order n) is a square matrix (of size n) for which in each column and in each row there is precisely one entry with value 1. All the other entries in the matrix are 0. There is two ways in which you can view a permutation σ of order n as a permutation matrix, the ‘column position’ point of view, and the ‘row position‘, where the ‘row position‘ point of view is the ‘column position’ point of view for σ-1, and, symmetrically, the ‘row position’ point of view for σ-1 is the ‘column position’ point of view for σ.
As we are interested in sudoku's and related grids, let's take a permutation (matrix) of order 9 as an example, say:
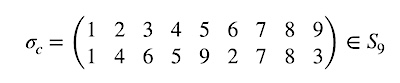
From column-position point of view, the corresponding permutation matrix, col(σ), is:

And this indeed, as you will easily check, is the permutation matrix from a row-position point of view of the permutation's inverse and vice versa, i.e., col(σ) = row(σ-1) and row(σ) = col(σ-1). The two matrices are each other's transpose, and each other's inverse, i.e. col(σ-1) = col(σ)-1 = col(σ)T, and row(σ-1) = row(σ)-1 = row(σ)T.
Instead of considering a numerical matrix, we may represent a permutation matrix by a grid in which we replace the number(s) by a symbol, or by a color:
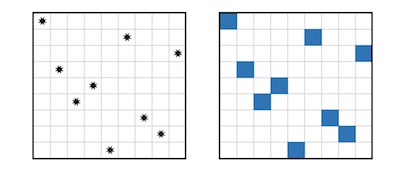
A sudoku solution and an order 9 latin square are both examples of what (e.g. in [ 1 ]) are called full sets of mutually disjoint permutation matrices of order 9: sets of nine permutation matrices such that their sum-matrix has a 1 in every cell, i.e. in each pair of distinct matrices P, Q from that set corresponding cells have at most one '1': P(i,j) × Q(i,j) = 0, for all pairs of indices (i,j).
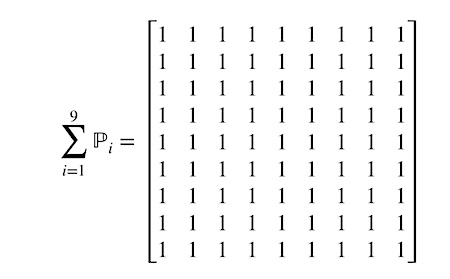
(added April 18th 2025 :) We can therefore dissect a sudoku solution (suso), and unfold it into its set of nine disjoint permutation matrices, which like the suso's nine voices. it is interesting and fun to visualize this decomposition.)
A full set of mutually disjoint permutation matrices of order 9 will always translate into an order 9 latin square. For it to also be a sudoku, the additional permutation constraint on the composite matrix' nine 3x3 squares needs to hold. If in a sudoku solution or an order 9 latin square we replace the numbers 1 to 9 by, e.g., nine different colors, here are two examples of grids that we may get:
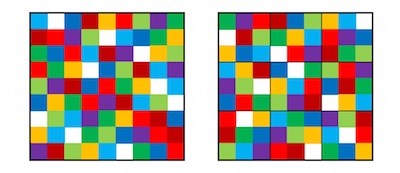
Do you see how the difference in entropy stands out, the difference in degree of order (of balance, of symmetry) between the two images? The left grid was obtained from an order 9 latin square: in the nine 3x3 squares into which the grid is divided, the same colour(s) appear(s) multiple times. This is not the case for the grid on the right, in which the color blocks at a glance of the eye appear instantly far more balanced, long before one finds out why that would be so: in the right image in each of the nine 3x3 squares all nine colours are present. It is a sudoku solution. Or, as we can assign the numbers 1 to 9 to the nine colours in 9! = 362880 ways, it rather are (sic) 362880 soduku solutions. Similarly, the order 9 latin square to the left are (sic) 362880 order 9 latin squares. Let us call these sets of 362880 grids, the full sets of colorations of the grids. Two distinct elements in these sets are each other's recoloration. So any sudoku solution, any order 9 latin square etc, has 362879 different recolorations.
A Perished Piano Sudoku Dream Machine
In one of my cherished recurrent dreams I outfit my late mother's perished piano with a player system that, controlled by a relatively simple script, would endlessly perform the '27+22 Variations', for all of the 362,880 different colourings of the initial sudoku solution. Placed in a secure and serene space (a chapel, perhaps, or museum) and given some regular technical and mechanical care, the perished piano would play the variations for an estimated duration of approximately 125 years.
This is a bigger-than-human-lifetime duration, but still an oversee-able one, and a period of time over which one may imagine keeping the old piano in a working state. Were one to also include all or some of the variants resulting from (combinations of) permutation of and within 3-blocks of rows (bands)/3-blocks of columns (stacks), from transposition, rotation, reflection in the middle column, middle row or in one of the two diagonals (all of these together form the group of symmetries of a sudoku solution), the number of 24/7 playing years will quickly run into the millions, time here floating into an utterly unimaginable future, whatever be our dreams and/or (il){de}lusions.

(The image is an edited montage of two DALL-E outputs on the prompt 'Perished Piano Sudoku Dream Machine' january 7th 2025)
Premutation meditations
I like that word: 'pre-mutation'.
Or 'premutation'.
It evokes a maybe-typo, a permutation of ‘permutation’—a state preceding change, preceding transformation, a prelude to plots yet to unfold, to knots to be unraveled—and as a word that invites deep thoughts if only you let it bring 'm in.
A key feature of the sudoku-generated pieces as I did them up till now is their touching on the extremes of, on the one side, the near to total determinism once a sudoku grid has been picked as its source, and, on the other one, the utter contingency of the choice of that particular sudoku solution, among the 6,670,903,752,021,072,936,960 (about six sextillon) ones that are available. {[()—Except, of course for the fact that I did choose not any other but that particular sudoku, any of the astronomical many different ones could equally well have been used to 'materialise’ (is there a better word? ... sort of like an observational collapse of a superposition of probabilities) this one among all possible pieces, like we live this one among all possible lifes, in this one among all possible worlds.—()]} That is the actual heart of the ‘Perished Piano Sudoku Dream Machine‘, and its proposed cycling through all of the 9! possible ways to ’name‘ by 1 to 9 the elements of the full set of permutation matrices that corresponds to the sudoku, of all its possible recolorations: it is an unfolding, a sequentialisation, of all possible worlds rather than the instantaneous collapse into a single one.
“war drift“ ( Sudoku 4, for violoncello )
After the first one, the ‘let me show you exactly who you are‘ for Shih-wen's double bass, these past weeks I scored a second sudoku solution for a traditional acoustic classical instrument, for the violoncello, planned to be premiered early this summer. The violoncello score follows the same pattern of interpretations of the sudoku solution as that for the double bass (and, very likely, for several other pieces yet to come). The main difference then is, obviously, the soduku solution used (it is sudoku2004, the one featured in the fourth week's K7 sudoku recording of 2020). Also, the 'diagonal sudoku' used for the separation of the sudoku solution in two sudoku puzzles, is a different one, and the initial movement chosen was not 'up', but 'down'.

(The image is a cut out part of a DALL-E output on the prompt 'realistic and atmospheric photo-like image of a single-turn ribbon with music notes, shaped like a ring, floating above a stormy, empty sea, slight slope, not touching the water' january 15th 2025)
Like the piano pieces, also these pieces are cyclic. Think of them as ‘looping‘, as closed ribbons, that for a recording or performance one might basically just cut open at any desired point, and perform the linearization thus obtained. The cello piece starts with the second (C) of the two 'filtered' parts, followed by the 'unfiltered' one (A, starting with the note that ends C) and ending with the first 'filtered' part (B, that starts with the note that ends—and starts— the A-part).
Here is a graphic rendering of the pitches-durations of the parts in the order proposed for a first performance (note how the piece indeed closes (pitchwise) onto itself, it is circle):
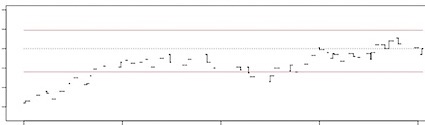 |
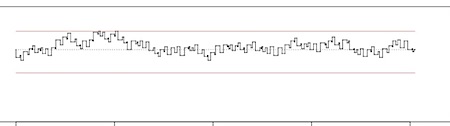 |
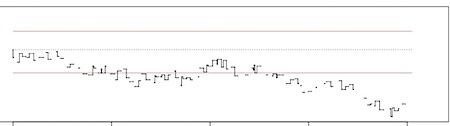 |
The parts that are outside the range of the cello, in this piece have been filled with words. Dutch words, that during a live performance are to be spoken by (at least) two voices, preferably by more (small choir), and preferably by Dutch speakers with strong local accent (Vlaams, Limburgs, Zeeuws ...). The text/poem, cyclic as is the music (its title is also the title of the full piece: war drift) can be found on Medium.
towards (?) costas sudokus
I am pretty sure there are more pieces to come in this cyclic form, though I doubt I will get to produce one for all of the fifty-two 2020 sudokus 😏, intend as I am to follow up on the divers trains of sudokist thoughts that—in a most entertaining manner, let me assure you— come and ago while playing around with, within and around these number grids.
Among these trains, one that I jumped on around the past Xmas days was due to reflections on picking out some among the astronomically many sudoku grids because of specific additional properties, either of the sudoku solution as a whole, or because of special properties of the order 9 permutations that they are made of. In ‘the early days‘ of K7-sudokus such properties were that of what I called the sudoku's drift (for those K7-plays ((with a reading that is what we might call the ‘occidental’ or ‘western‘-way: as a left-to-right / top-to-bottom +/- walk)) the drift is the difference between the sudoku-walk's starting point and its end point) and that of its stretch (the difference between the walk's max on the positive side, and its min on the negative side), the details are in one of the early sudoku writings.
This then had me revisit another one of my pre-mutation pre-occupations namely that of costas arrays. At the time I looked into these, sudokus actually were far from my mind, but now I asked myself, would it be possible, to find sudoku solutions in which all rows and columns, and maybe even the squares' in some reading, have the costas property?
The answer is 'no'. At least in the sense that there can be no suduko solution such that all rows (and hence, by transposition such that all columns) have the costas property. We learn from e.g. reference [1] that, at least up to order 27, for uneven numbers u, the largest number of disjoint costas arrays of order u is less than u. Hence for uneven orders up to 27 there are no full sets of disjoint costas arrays. Therefore there are no costas latin squares of, in particular, order 9. As a suduko solution is always also a latin square, this implies that there are no sudoku solutions where all rows and/or all columns have the costas property. (This does not seem to imply the non-existence of sudoku solutions such that in a certain reading all of its 9 sub-squares have the costas property; or does it? The ‘a certain reading‘ is somewhat on the vague, and the strong connection with the permutation matrices of course is lost.)
costas 12-sudokus
But for some even orders we do find such full sets, in particular for the (from a music-compositional point of view) interesting order 12. The reference [1] gives the (computationally obtained) results that the largest number of disjoint costas arrays of order 12 is 12, and that there are 16,346 costas latin squares. The authors of reference [1] understand a ‘costas latin square’ to be the superposition of the disjoint permutation matrices, which is (sort of) equivalent to a costas latin square in our sense, as taking the disjoint costas arrays as the rows or as the columns of a grid, conserves the latin property of the grid, and obviously the costas property is obtained for, at least, the rows of the grid.
We can design, in (at least) two variants, of what would be a latin square of order 12 that may count as an order 12 sudoku. Here are examples, in the form of color grids. Note that they are (rotationally) equivalent.
 |
 |
Using the fact that (what I called) a cyclic latin square can be made into a sudoku by a permutation of rows or columns (see The Art of K7 :: Südokaising [i]), and the Welch construction of costas arrays (of order q-1 for prime numbers q) that are (what I called) cyclic (‘single periodic’ i.e. cycling them conserves the costas property, see ‘The eerie symmetry of a perfect ping’) it is easy to construct a set of order 12 sudokus, such that all of the sudoku's rows or all of the sudoku's columns have the costas property.
In the sudoku(s) thus obtained from the order 12 costas sequence generated by the number 2 (the smallest primitive root of GF(13), it is the sequence of the first 12 powers of 2 —21, 22, ..., 211, 212— all modulo 13) even more than the expected minimal number of costas arrays (12) popped up. Here are the two costas latin squares obtained, by cycling the rows as if they were wheels on a vertically oriented cylinder, or the rows as if wheels on a horizontally oriented cylinder:
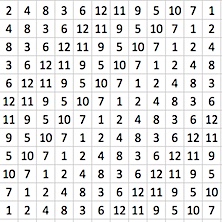 |
 |
The initial costas sequence is the first row (the first column) in the grids; the latin square on the left then is obtained by cycling the row to the left (cycling the column úp), a single step per ‘tick’ (next row:next column); the one on the right by cycling the row to the right (cycling the column dówn), a single step per ‘tick’ (next row:next column). If we use the rows for the cycling, they generate their copies in the columns;  if we use the columns for the cycling, they generate their copies in the rows. {{ Imagine the sudoku grid made into the surface of a torus! }} Each row and each column of the two grids is obtained as cyclic variation of the initial sequence, and all of them therefore have the costas property.
if we use the columns for the cycling, they generate their copies in the rows. {{ Imagine the sudoku grid made into the surface of a torus! }} Each row and each column of the two grids is obtained as cyclic variation of the initial sequence, and all of them therefore have the costas property.
But then this is the sudoku obtained from the left variant above, by applying the permutation σ(1:12)=(1, 5, 9, 2, 6, 10, 3, 7, 11, 4, 8, 12) to its columns:
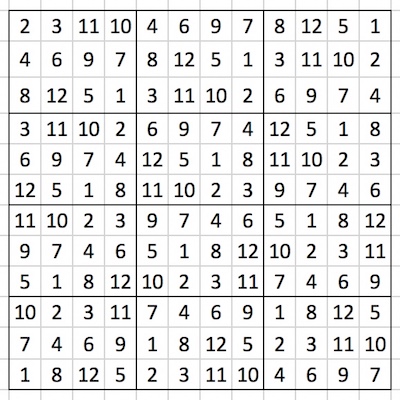
In this sudoku the rows of the original grid are ‘messed up‘, but all costas columns are still there; also all the rectangles, when read column-wise in ‘western way‘ (that is, from top-to-bottom, left-to-right) correspond to costas arrays from the latin square. We see e.g. that thus written the first rechtangle linearizes to the initial costas array, and all the others, counted from left-to-right, top-to-bottom, will linearize to the rows of the left variant costas latin square.
The costas arrays that make up this 12-sudoku are none other than the 12 cycles of the initiating exponential Welch costas array. There are, however, two other costas arrays in this grid: also the sixth and the twelfth row, (12,5,1,8,11,10,2,3,9,7,4,6) and (1,8,12,5,2,3,11,10,4,6,9,7) have the costas property. These, however, are not cyclic (single periodic). It is as yet unclear (to me :) whether these ‘costas appearances’ here are necessary, and a consequence of the construction applied; or is it mere chance, a coincidence? {{(à voir ... costas permutations are rare: there are 7825 order 12 costas permutations, on a total of 12! order 12 permutations, which makes the chance to pick one of them at random about 0.00001633 )}}. The same costas arrays appear when we apply the permutation σ(1:12)=(1, 5, 9, 2, 6, 10, 3, 7, 11, 4, 8, 12) to the rows of the left variant (the result of this operation is the transpose of the above grid), to the columns of the right variant, or (in the 5th and 11th column, top to bottom) when we apply the permutation σ(1:12)=(1, 5, 9, 2, 6, 10, 3, 7, 11, 4, 8, 12) to the rows of the right variant. Here the cycles of the initiating exponential Welch costas array make up the rows and the rectangles (read left-to-right, from bottom row to top row) of the sudoku grid.
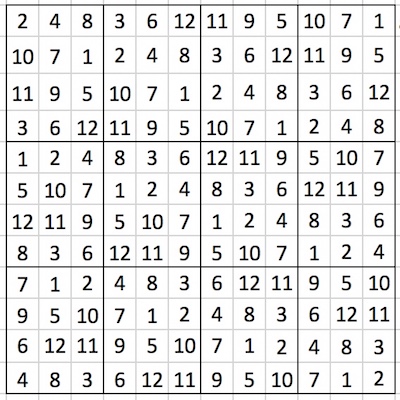
One feels, of course that these four costas 12-sudokus that we made, will be equivalent, in the sense that a given one can be transformed into another by a some sequence of permutations of its rows and columns. Also the four obtained starting from the costas array generated by 7, the multiplicative inverse modulo 13 of 2 (which is a cyclic variation of the one generated by 2) fall somehow in that same league, and they do not come with the (same) two ‘extra‘ costas permutations that were brought to us by 2 above.
This, however is not the case for the 12-sudokus that we obtain using the other pair of complementary primitive roots in GF(13), the pair (6,11). Here there is no additional surfacing of costas arrays.
The four-ness of it all, it almost shouts out that somewhere in there must a quartet of some sort 🤓 ...
how we get more costas from a cyclic costas latin square and what that has to do with 3d latin and sudoku boards
It is interesting and useful to think of latin squares and sudokus of order n kind in a 3d manner, as mappings f : N × N → N. The grids are sets of triples (i, j, k) ∈ N × N × N satisfying certain properties (where N denotes the set of integers {1,2,...,n}). One can visualise them
(as in the picture, which is the central part of an output generated by DALL-E ((25 Jan. 2025)) on the prompt 'three dimensional sudoku,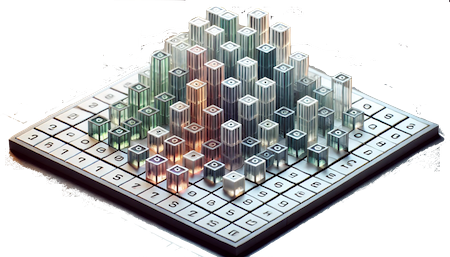 where the grid is the two dimensional base, like a chessboard of 9 x 9 fields, and the numbers in the cells denote the height of blocks that are placed on those fields') as blocks of differing heights on a chess-like board. A bit more about that, soon, in a next sudoku SB- text! 🤓
where the grid is the two dimensional base, like a chessboard of 9 x 9 fields, and the numbers in the cells denote the height of blocks that are placed on those fields') as blocks of differing heights on a chess-like board. A bit more about that, soon, in a next sudoku SB- text! 🤓
—to be continued—
references __ ::
[1] J.H. Dinitz, P.R.J. Östergård, D.R. Stinson (2021). “Packing Costas Arrays” [
^ ]
Read all about Sudokism and Südokaising on the SoundBlog:
(2025, april 18) - A decom-.pomdipem~padopi~dompadé.-posed suso
(2025, march 01) - Full coloration set sudoku solution pieces
(2025, january 23) - ‘War drift’ for violoncello, and other sudoku, latin and costas grids
(2025, january 3) - “Let me show you exactly what you are” (Sudoku 3, for double bass)
(2024, july) - Uit de kast: "I am a Sudokist!"
(2021, september 11) - The Art of K7 :: Südokaising [ii] Time Folds
(2020, march 21) - The Art of K7 :: Südokaising [i]
(2006, april 17-25) - 'sudoku-solution' in 'de nor'
Read about Sudokism and Südokaising on Medium:
(2024, october) - Variations on a Sudoku Solution for Perished Piano
tags: sudokism, permutations, costas permutations, latin squares
# .550.